手機直線：
咨詢熱線：0571-56211150
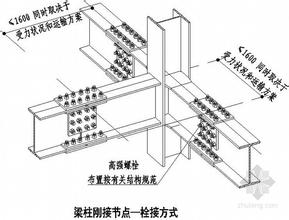
近十幾年來，多層鋼框架和門式剛架輕型鋼結構在我國廣泛應用，端板連接也隨之在工程中大量采用。梁柱節點受力特性對鋼框架的受力特性有很大影響。當同時考慮 P-∆效應時，節點變形可能導致鋼框架產生較大的水平側移。對于大多數梁柱連接節點，與轉動變形相比，軸向變形與剪切變形都很小，因此，從實用的目的，只需考慮連接的轉動變形。轉動變形習慣用連接彎矩的函數來表達。
在很多情況下，鋼結構端板連接屬于半剛性連接。對于半剛性連接，歐洲規范要求有節點的彎矩-轉角(M-φ)設計曲線作為依據，且承受設計的內力。我國鋼結構設計規范提出：梁與柱的半剛性連接只具有有限的轉動剛度，在承受彎矩的同時會產生相應的轉角，在內力分析時，必須預先定連接的彎矩-轉角(M-φ)特性曲線，以便考慮連接變形的影響。但是，新規范并沒有給出半剛性連接的具體設計有限元分析計算方法。所以，研究半剛性連接彎矩-轉角(M-φ)特性就顯得很有必要。
但是，端板連接由于自身構造特點，其構造形式種類繁多，可變的幾何參數也很多，例如：平齊式和外伸式、外伸式端板在梁受拉翼緣一側外伸或者在梁上下翼緣兩側均外伸、節點域有無加勁肋、端板外伸部分有無加勁肋、螺栓的行數和列數、端板厚度、螺栓直徑和等級、螺栓預拉力大小、螺栓位置、梁柱截面尺寸、端板摩擦面抗滑移系數等等。所以，要想完全通過試驗來確定各種形式和構造的端板連接的彎矩-轉角(M-φ)特性很難實現。而且，端板連接的很多受力特性，例如：螺栓的具體受力狀態和受力大小、柱翼緣和端板之間接觸狀態、摩擦力的大小和分布、節點變形具體來源、端板變形狀態、杠桿力的大小和分布等， 在現有技術條件下，很難通過試驗測量得到結果。
隨著有限元理論和計算機技術的發展，對端板連接的受力特性進行非線性有限元計算成為可能。而且，有限元計算一旦經過試驗驗證，將是一種獲得端板連接受力特性的安全、可靠、合理、便捷而且經濟的方法，能夠很好地彌補試驗測量條件的局限性，從而獲得對鋼結構端板連接受力特性更準確、更全面的認識。
專業從事機械產品設計│有限元分析│強度分析│結構優化│技術服務與解決方案
杭州納泰科技咨詢有限公司
本文出自杭州納泰科技咨詢有限公司m.xiangzuoxiangyou.cn，轉載請注明出處和相關鏈接！